Pythagoras and Musical Scales

The Greek Pythagoras was known mainly for his discoveries and creations on mathematics. But there is a fascinating story regarding his research on musical notes. Pythagoras wanted to see if there was a way to relate musical notes with string lengths. He made the fascinating discovery that it was the simplest fractions of the original string length that produced the most consonant - or pleasing - sounds.
I discuss his findings below. My intention is to provide one of the simplest and (hopefully) most understandable presentation possible. For this reason I won't be switching between "fractions" and "ratios", like most of the numerous articles I've read. It'll be just fractions.

1) Pythagoras first tried (probably not for long) comparing the original string length's sound to itself (the "Unison"). Pluck the string and then pluck it again, and/or pluck two strings of the same length at the same time.
Boring.
He then moved to the next step, which was to divide the original string in half. So he compared the sounds of the two strings, the original and the shortened one. He found that these two sounds were the second most "consonant" when played simutaneously. He likely noticed that the two notes were somehow the same, even though the second was "higher".
Note that the first string can be any length. It is the fractional ratio that is important. If the second string is one half the length of the first one, the sound of both plucked together would be consonant.
We chose the modern note C4 to represent the first string, and we will be using modern note names for the other notes as well. And we use the modern values of the various note wavelengths to verify Pythagoras' discoveries using his fractions.
At the time Pythagoras did all this, there were 7 notes in the "diatonic" music collection ("scale") which existed then. So he noted that the second note was somehow the point where notes "repeat". So he called this note the "diapason" - the 8th note (of the existing scale) - or what we would call the "octave".
In our example, the note C5 on a piano is one octave above C4, and its wavelength (65.93 cm) is 1/2 of that of C4 (131.87 cm).

2) The next thing Pythagoras did was to look or the next simplest fraction. He already did 1/2, so the next thing fraction to try was 2/3. He found that, whereas the sound of the 1/2 length string was "similar" to the sound of the full length string, the sound of this string plucked by itself was "different". Also, playing the original string along with one that was 2/3 of its length also produced a more consonant sound. But this combined sound was far more interesting!
This is the note "G" on a modern piano keyboard, and is the magic "perfect fifth". It's called the perfect fifth because G is 5 white keys from C. Pythagoras called it the "Diapente" (5th note). Further, this note is based on second most simple fraction (next to 1/2) of the original string length.
The wavelength of G is 88.01 cm, which is 2/3 of the original C4.

"But what about 1/3?", you might ask. Isn't that "simpler" than 2/3? All the articles about Pythagoras that I've seen leave out 1/3 (and 1/4). Why is that?? Well, I'll discuss this below.

Here's the C4, the G, and then the two notes combined.

Here's the C4, followed by the C5, followed by both played together. The instrument is a Lyon and Healy harp - from the Garritan Harps collection.

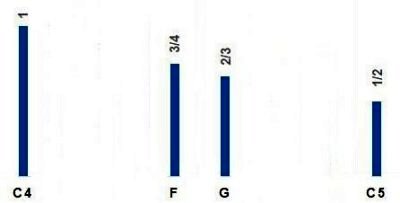
3) "What's next?", the Pi Man asked. He tried 3/4, and found that it, too, provided a consonant tone when played with the original string. It wasn't as powerful and primal as the perfect fifth, but was still better than any combination of strings involving fractions more "complex" than 1/2, 2/3, and 3/4.
This is the note "F" on a modern piano keyboard, and is the "perfect fourth", being 4 white keys from C. Pythagoras called this note the "Diatessaron" (4th note), not to be confused with the blue Infinity Stone Tessaron!
The wavelength of F is 98.79 cm, which is 3/4 of the original C4.

And what about 1/4 (and 1/3)? See the next panel.

Here's the C4, the F, and then the two notes combined.

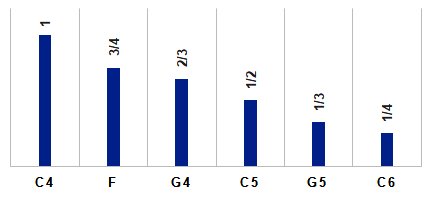
4) So THIS shows why 1/3 and 1/4 were not used in deciding what fractions should be used as the simplest ones based on the original string. It turns out that 1/3 and 1/4 of the original string produced notes that were contained in higher octaves.
So if we use the modern C4 as the "original string":

The wavelength of C4 is 131.87

1/3 of 131.87 yields 43.9, which is the wavelength of the G5 that is above C5.

1/4 of 131.87 yields 32.96, which is the wavelength of C6 which is one octave above C5, and 2 octaves above the original C4.

So perhaps Pythagoras, upon hearing that these two new notes were "higher" than C5, concluded that these two notes were "out of range" of the original octave from C4 to C5. So perhaps he simply decided to use 1 minus 1/3, or 2/3, and 1 minus 1/4, or 3/4 as the next simplest fractions between 1/2 and 1.
One other possibility is that he saw that 1/3 of the original string length yielded a note that was in the second octave, so multiply by 2 to move it back to the original octave, yielding 2/3. Similarly, if 1/4 of the original string length led to a note in the third octave, multiply it by 3 to move it back to the original octave, yielding 3/4.
In any case, using what we know today about frequencies and wavelengths, we have:

2/3 of 131.87 yields 98.9, which is the wavelength of the modern note G (above C4).

3/4 of 131.87 yields 87.9, which is the wavelength of the modern note F, above C4

And here is: C4, then G5, back to G4, followed by C4, then C6, back to F4

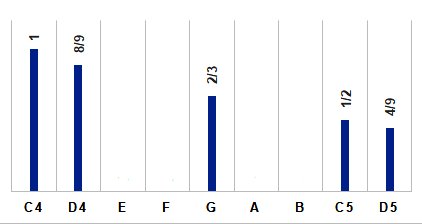
5) So, as of section 3 above, we (and Pythagoras) have 4 notes:

C4 (representing string length 1),

F (3/4 of the original string length - the "Perfect Fourth"),

G (2/3 of the original string length - the "perfect Fifth"),

C5 (1/2 of the original string length - the "Octave"),

So how did Pythagoras derive the remaining fractions, in his efforts to show that music was somehow related to basic - or relatively basic - fractions?
Pythagoras might have reasoned that, if 2/3 of the original string length produced such a harmonic note, what if we take 2/3 of the F and the G that we have already created, and use this to create more notes.

So we take 2/3 of G. To do this we multiply "G" (which is 2/3 of the original string) by 2/3. That is, we are finding the "perfect fifth" of G. On a modern piano keyboard, this is 5 notes above the G.

So 2/3 X 2/3 gives us 4/9, which is D5 in the above image.

To move the D back to the original octave, we multiply by 2. This gives us 8/9, which became the (relatively) simple fraction that Pythagoras associated with D. This is D4.

"How did the Pi Man know this?", you might ask. Perhaps by comparing sounds with existing instruments. But we can verify using modern concepts. Thus G (wavelength 88.01) X 2/3 is 58.67. This is the wavelength of D5 that is one octave up. To move it back to the original octave, multiply by 2, and we get 117.34, which is D4 in the original octave.

This just might be the origin of the "Circle of Fifths", which has to be the most confusing diagram on the planet!

And here is: C4, then D5, back to D4, followed by the sequence C4, D4, G, C5

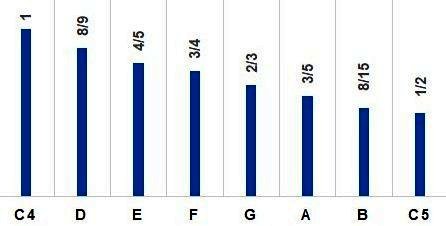
6) In the image above, we see the 7 notes of the diatonic collection. The fractions that are shown represent what are believed to be the original ones that Pythagoras came up with.
So we have already created D by taking 2/3 of G, which gave us a D in the next octave. Multiply by 2 to move it back to the original octave.

We now take our D (8/9) and multiply by 2/3. So 2/3 X 8/9 = 16/27. This fraction can't be simplified, but it's "close" to 15/25, which simplifies to 3/5. This creates the note "A". As a "sanity check", 16/27 is .5926, and 3/5 is .60.

Sound a bit sloppy? It is, but it is well to note that while our musical notes are fairly precise today, the diatonic scales back in Pythagoras' time were highly variable, and were said to be different even from one city to another.

Now we take our A (3/5) and multiply by 2/3, yielding 6/15, which simplifies to 2/5, which is E in the next octave. Multiply by 2 and we get 4/5, the "E" in the original octave.

Finally, we multiply E (4/5) by 2/3 and we get 8/15, or "B".

We can check all this using the "modern" wavelengths of the various notes. (Remember that all modern notes have been "adjusted" from Pythagoras' time, to provide equal spacing between notes. So these numbers differ slightly from those you might calculate using the Pythagoran fractions.)

So G (wavelength 88.01) X 2/3 is 58.67, which is D, but one octave up. So multiply by 2 and we get 117.34, which is D in the original octave.

Now we take D (wavelength 117.34) X 2/3 is 78.23, which is A in the original octave.

Now we take A (78.23) X 2/3 is 52.15 which is E, but one octave up, So multiply by 2 and we get 104.31, and we get E in the original octave.

And finally we take E (104.31) X 2/3 and we get 69.77, which is B.

And finally, the entire "C major pitch collection"

Another excellent summary on the origins of musical notes can be found here:

Where Does the 12-Tone Scale Come From

And here's "Jimmie's Diatonic Chart". Each line shows:

The note name for each note, or "scale degree"

The Pythagoran string fraction

The frequency, as adjusted for modern notes. The frequency doubles for any octave, E.G.: C to C, G to G, etc.

The wavelength, as adjusted for modern notes. The wavelength is halved from octave to octave.

NOTE	Note Name	String Length	Frequency	Wavelength
C4	Tonic	1	261.63	131.87
D	Supertonic	8/9	293.66	117.48
E	Mediant	4/5	329.63	104.66
F	Subdominant (Perfect 4th)	3/4	349.23	98.79
G	Dominant (Perfect 5th)	2/3	392.0	88.01
A	Submediant ("Concert A")	3/5	440.0	78.41
B	Leading Tone	8/15	493.88	69.85
C5	Octave	1/2	523.25	65.93
D-F
G	Pf 5th oct	1/3	783.99	44.01
A-B
C6	Octave	1/4	1046.5	32.97

As a final note, string lengths and the resulting musical notes are proportional, for "simple" strings. If you pluck a string and then hold your finger in the middle and pluck one of the halves, you will get a note an octave higher. So you could potentially make a simple string instrument using these simple fractions.

So, you wanna' make your own harp? Then you need Gamut Strings' site:

Gamut Strings Quick Calculator

But the string proportionality is not true of pipes. Thus if you were making wind chimes, you can't just cut a pipe until it sounds like "C" and then cut another pipe 2/3 that length in order to get "G". There are actually charts for cutting pipes, and their lengths are not simple proportions like those of strings. The lengths even change for different metals and/or different wall thicknesses.

What? You want to make wind chimes instead? Then you need Lee Hite's site:

Lee Hite's Say It With Chimes